How To Draw Shear Diagrams And Moment Diagram For A Beam

Shear and Moment Diagrams – An Ultimate Guide

In this post nosotros're going to take a look at shear and moment diagrams in detail. Determining shear and moment diagrams is an essential skill for any engineer. Unfortunately information technology's probably the 1 structural analysis skill most students struggle with most.

This is a problem. Without understanding the shear forces and bending moments developed in a construction you tin can't complete a design. Shear forcefulness and bending moment diagrams tell us about the underlying state of stress in the construction. So naturally they're the starting point in any pattern procedure.

Some other reason every graduating engineer needs to have a solid grasp of shear forces and bending moments is considering they're admittedly going to be tested in almost every graduate interview. The quickest way to tell a keen CV writer from a groovy graduate engineer is to enquire them to sketch a qualitative bending moment diagram for a given structure and load combination!

So in this mail service nosotros'll give you a thorough introduction to shear forces, bending moments and how to draw shear and moment diagrams. We won't be able to cover everything in this one mail service but hopefully you'll reach the stop knowing more than than when you started! If y'all want to practice a deep swoop to actually nail downwards this skill, you should have a look at my course, Mastering Shear Strength and Angle Moment Diagrams [🎓 NOW FREE FOR STUDENTS]. In it, nosotros'll cover the fundamental theory and put it into practice with enough of worked examples.

In this post we'll cover…

Download the DegreeTutors Guide to Shear and Moment Diagrams eBook. 📓
Mastering Shear Forcefulness and Bending Moment Diagrams
- Your complete roadmap to mastering these essential structural analysis skills.
1.0 What is a Angle Moment?
2.0 What is a Shear Strength?
3.0 Computing Internal Shear Forces and Angle Moments
4.0 Edifice Shear and Moment Diagrams
- four.i Finding the location of the maximum angle moment
5.0 Cartoon Shear Strength and Bending Moment Diagrams – An Example
- 5.i Video Tutorial
- 5.2 Calculating the support reactions
- 5.3 Drawing the shear force diagram
- five.4 Cartoon the bending moment diagram
6.0 Relating Loading, Shear Force and Bending Moment
- 6.one Case one: Uniformly distributed loading
- 6.ii Case 2: Signal force loading
- six.3 Case 3: Betoken moment loading
7.0 Another Example
- seven.ane Setup and shear force diagram
- 7.2 Building the bending moment diagram
- 7.3 Confirming maximum moment with calculus
Build your own shear force and angle moment solver
Axle & Frame Assay using the Direct Stiffness Method in Python
- Build a sophisticated structural assay software tool that models beams and frames using Python.
Tutorial by:
Dr Seán Carroll

ane.0 What is a Bending Moment?

Permit's start with a basic question; what is a bending moment? To reply this we need to consider what's happening internally in a structure under load. Consider a but supported beam subject to a uniformly distorted load.

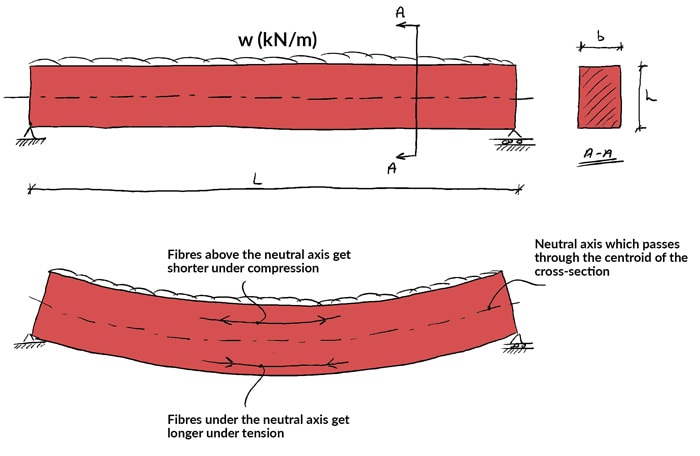
Shear-and-moment-diagrams-beam | DegreeTutors.com

The beam will deflect under the load. In order for the axle to deflect as shown, the fibres in the acme of the beam must contract or become shorter. The fibres in the bottom of the beam must become longer.

Nosotros can say the height of the beam is in compression while the bottom is in tension (observe the management of the arrows on the fibres in the deflected beam). Now, at some position in the depth of the beam, compression must plough into tension. There is a aeroplane in the beam where this transition between tension and compression occurs. This airplane is chosen the neutral plane or sometimes the neutral axis.

Imagine taking a vertical cut through the axle at some altitude $x$ forth the axle. We tin can represent the strain and stress variation throughout the depth of the beam with strain and stress distribution diagrams.

Shear-and-moment-diagrams-stresses | DegreeTutors.com

Remember, strain is just the change in length divided past the original length. In this instance we're considering the longitudinal strain or strain perpendicular (normal) to the cut face.

Pinch strains to a higher place the neutral axis exist because the longitudinal fibres in the beam are getting shorter. Tensile strains occur in the bottom because the fibres are extending or getting longer.

We can presume this axle is made of a linearly elastic textile and as such the stresses are linearly proportional to the strains. This only ways we demand to multiple the strain at some indicate in the beam by the Immature'southward modulus (modulus of elasticity) to get the respective stress at that point in the axle.

We know that if we multiply a stress by the area over which information technology acts, we go the resultant force on that surface area. The same is true for the stress interim on the cut face of the beam. The compression stresses can be represented past a compression force (stress resultant) while the tensile stresses can be replaced by an equivalent tensile forcefulness. So for example the compression forcefulness is given by,

(one) $\begin{equation*} F_c = \underbrace{\left[\sigma_t \times \frac{1}{2} \right]}_{\text{average stress}}\underbrace{\left[ b \times\frac{h}{2}\right]}_{\text{area}} \end{equation*}$

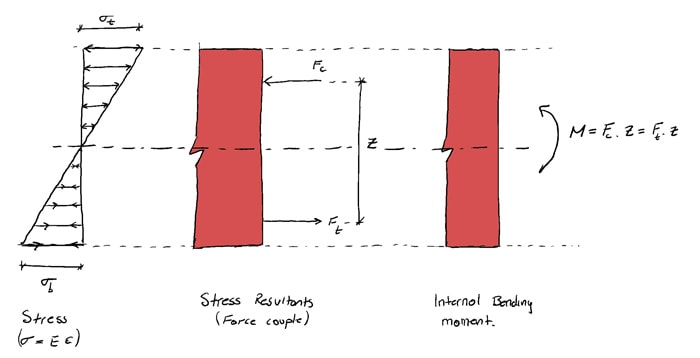
Shear-and-moment-diagrams-force-couple | DegreeTutors.com

As a result of the external loading on the structure and the deflection that this induces, we end up with two forces acting on the cut cross-department. These forces are:

equal in magnitude (must be to maintain force equilibrium)
parallel to each other (and perpendicular to the cut face)
acting in opposite directions
separated past a distance or lever arm, $z$

You might recognise this pair of forces every bit forming a couple or moment $M$ .

(two) $\begin{equation*} M = F_c\times z = F_t\times z \end{equation*}$

💡 The internal bending moment $M$ , is the bending moment we represent in a angle moment diagram. The bending moment diagram shows how $M$ (and therefore normal stress) varies beyond a structure.

If we know the country of longitudinal or normal stress due to bending at a given section in a structure we can work out the corresponding angle moment.

However, more often information technology's the instance that we know the value of the bending moment at a indicate and use this to work out the maximum values of normal stress at that location.

We practise this using the Moment-Curvature equation a.k.a. the Engineer'southward Angle Equation…

(3) $\begin{equation*} \boxed{\sigma = \frac{-M\:y}{I}} \end{equation*}$

…which relates the stress, $\sigma$ at a distance $y$ from the neutral axis, to the moment, $M$ . Where $I$ is the second moment of area for the cantankerous-section.

Hopefully now you can conspicuously run across how bending moments arise;

external forces induce deflections
strains develop (which we see at a larger scale equally structural deflections)
where nosotros have strains, we must accept stresses (retrieve Young's modulus)
these stresses, can exist represented with their forcefulness resultants that ultimately grade a couple or internal bending moment, $M$

2.0 What is a Shear Strength?

We tin at present turn our attention to shear forces and get-go with a simple definition;

💡 A shear force is any force acting perpendicularly to the longitudinal centrality of the construction. We're typically interesting in internal shear forces that are the resultant of internal shear stresses developed in the structure.

Building on our give-and-take of bending moments, the shear force represented in the shear forcefulness diagram is also the resultant of shear stresses interim at a given point in the structure. Consider the cut face of the axle discussed above.

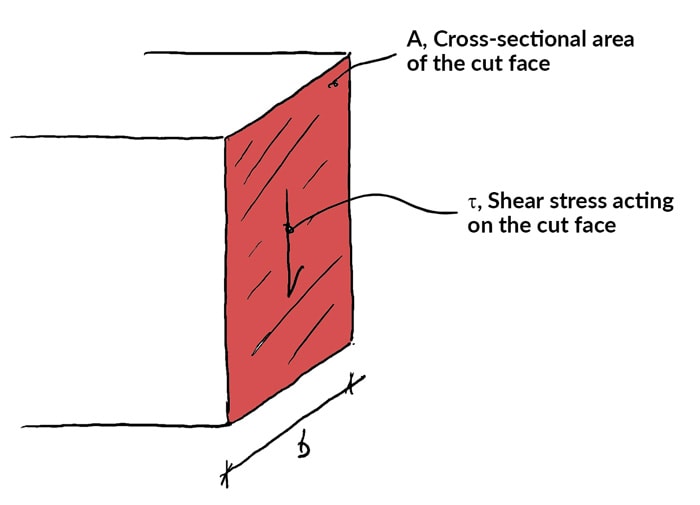
Shear-and-moment-diagrams-force-shear-stress | DegreeTutors.com

The shear stress, $\tau$ acting on this cutting face up is evenly distributed across the width of the face and acts parallel to the cut face up. The average value of the shear stress, $\tau_{avg}$ is simply the shear force at this point in the structure $V$ divided by the cantankerous-sectional surface area over which it acts, $A$

(iv) $\begin{equation*} \tau_{avg} = \frac{V}{A} \end{equation*}$

However, this is merely the average value of the shear stress acting on the face. The shear stress actually varies parabolically through the depth of the section according to the following equation,

(five) $\begin{equation*} \tau = \frac{VQ}{Ib} \end{equation*}$

where, $Q$ is the showtime moment of area of the surface area above the level at which the shear stress is being determined, $I$ is the 2nd moment of surface area of the cross-section and $b$ is the width of the section.

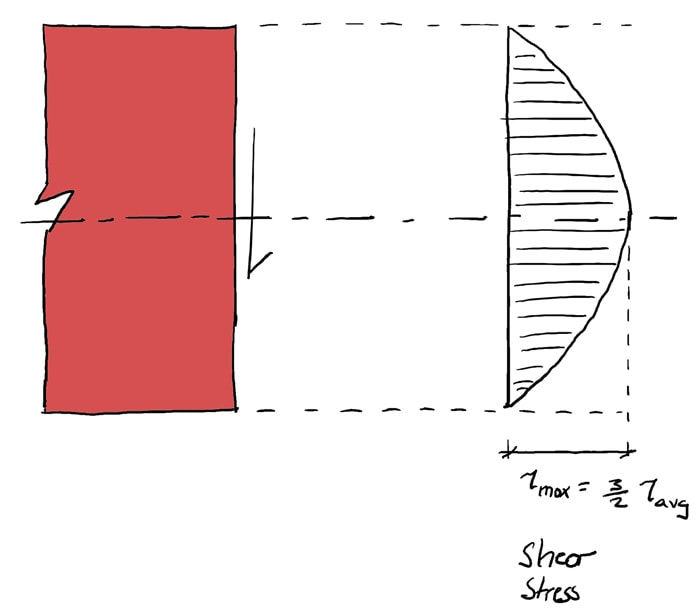
Shear-and-moment-diagrams-force-parabolic-shear-stress | DegreeTutors.com

We don't want to go likewise far downwardly the rabbit hole with shear stresses. For the purposes of this tutorial, all nosotros want to do is establish the link between the shear force we observe in the shear force diagram and the corresponding shear stress within the structure. Equations (four) and (5) do that for u.s.a..

iii.0 Calculating Internal Shear Forces and Bending Moments

Upwardly to this point nosotros've considered the link between the normal (angle) stress and associated bending moment and the shear stress and associated shear force. Based on this you should be comfortable with the idea that knowing the value of bending moment and shear force at a point are of import for agreement the stresses in the structure at that point.

Now we're going to consider the problem of calculating shear forces and bending moments not from the point of view of internal stresses but by considering equilibrium of the structure.

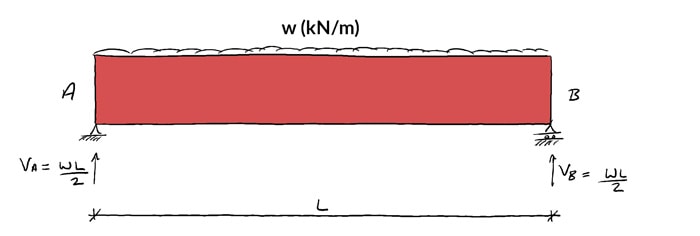
In reality, this is practically how nosotros determine the shear force and bending moment at a point in the structure. Again, let'due south consider the simply supported axle from in a higher place, subject to a uniformly distributed load, $w$ kN/chiliad.

Simple statics tell us that if the beam is in a country of static equilibrium, the left and right paw support reactions are,

(6) $\begin{equation*} V_a = V_b = \frac{wL}{2} \end{equation*}$

Shear-and-moment-diagrams-beam-udl | DegreeTutors.com

If the structure is in a land of static equilibrium (which it is), so whatsoever sub-construction or role of the structure must also be in a country of static equilibrium under the stabilising action of the internal stress resultants.

This is a key point! Imagine taking a cut through the structure and separating information technology into 2 sub-structures. When we cut the structure, we 'reveal' the internal stress resultants (bending moment and shear force).

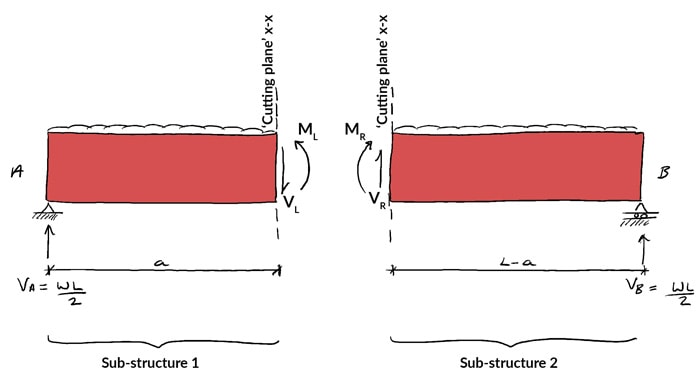
Shear-and-moment-diagrams-sub-structure | DegreeTutors.com

$M_L$ and $M_R$ are the internal bending moments on either side of the imaginary cut while $V_L$ and $V_R$ are the internal shear forces on either side of the imaginary cutting.

💡 $M_R$ and $V_R$ correspond the influence of the left manus side of the structure (sub-structure ane) on the correct paw side of the structure (sub-structure ii) and vice versa.

We've just said that each ane of these sub-structures is stabilised past the influence of the internal bending moment and shear force revealed by the imaginary cuts.

This ways, if we want to find the value of internal bending moment or shear forcefulness at any point in a structure, nosotros only cut the construction at that bespeak to expose the internal stress resultants ( $M$ and $V$ ). Then calculate what values they must have to ensure the sub-structure remains in equilibrium! For example the sub-structure beneath must remain in equilibrium under the combined influence of:

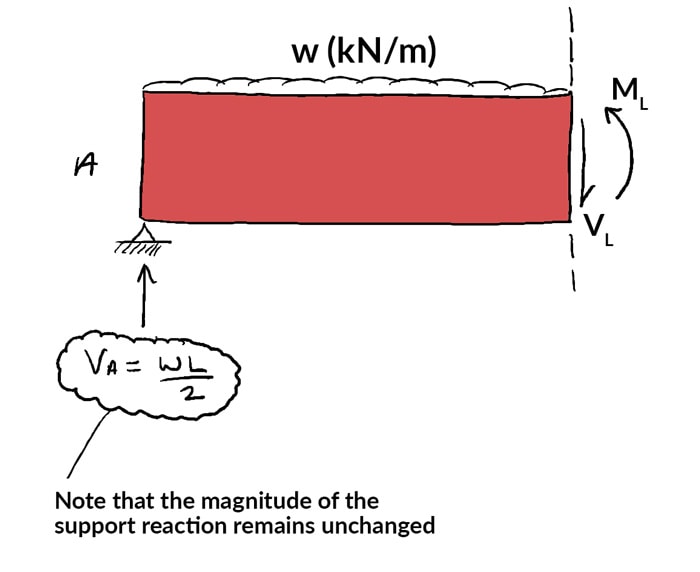
Shear-and-moment-diagrams-sub-structure-1 | DegreeTutors.com

This starts to brand more sense when we plug some numbers into an example. For the beam above, allow's imagine it has a bridge $L=6$ m, applied loading of $w=10$ kN/g and imagine we cut the axle at $a=2$ one thousand from the left hand support.

The left mitt reaction, $V_A$ is,

(7) $\begin{equation*} V_A = \frac{w L}{2} = \frac{10\times 6}{2} = 30 \:\text{kN} \end{equation*}$

At present taking the sum of the moments about the cut and assuming clockwise moments are positive,

(viii) 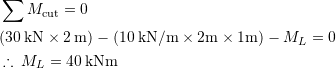$\begin{align*} &\sum M_{\text{cut}}=0\\ &(30\:\text{kN}\times 2\:\text{m}) - (10\:\text{kN/m}\times 2\text{m}\times 1\text{m}) -M_L=0\\ & \therefore \: M_L = 40 \:\text{kNm} \end{align*}$

So, the internal bending moment required to maintain moment equilibrium of the sub-structure is $40$ kNm. Similarly, if we take the sum of the vertical forces acting on the sub-structure, this would yield $V_L = 10$ kN.

4.0 Building Shear and Moment Diagrams

In the last section we worked out how to evaluate the internal shear force and angle moment at a discrete location using imaginary cuts. But to describe a shear force and bending moment diagram, we demand to know how these values change across the structure.

What nosotros really want is an equation that tells the states the value of the shear force and bending moment as a function of $x$ . Where $x$ is the position forth the axle. Consider making an imaginary cut, just like higher up, except at present we can make the cut at a altitude $x$ along the beam.

At present the internal shear force and bending moment revealed by the cut are functions of $x$ , the cut position. Here, we'll determine an expression for $M(x)$ . Only the procedure is exactly the same to decide $V(x)$ .

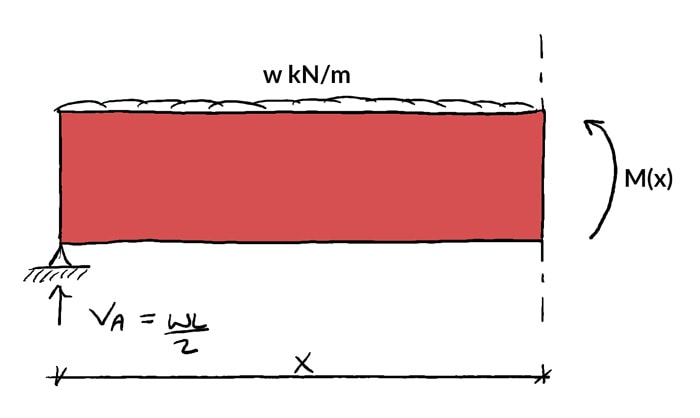
Shear-and-moment-diagrams-BMD | DegreeTutors.com

Taking the sum of the moments near the cutting and once again assuming clockwise moments are positive,

(9) $\begin{equation*} \sum M_{\text{cut}}=0 \end{equation*}$

(10) $\begin{equation*} \frac{wL}{2}x - w x \frac{x}{2}-M(x) &= 0\\ \end{equation*}$

(11) $\begin{equation*} M(x) &= \frac{wLx}{2} - \frac{wx^2}{2}\\ \end{equation*}$

(12) $\begin{equation*} M(x) &= \frac{wx}{2}(L-x) \end{equation*}$

Now we can apply equation (12) to determine the value of the internal angle moment for whatever value of $x$ along the beam. Plotting the bending moment diagram is merely a affair of plotting the equation.

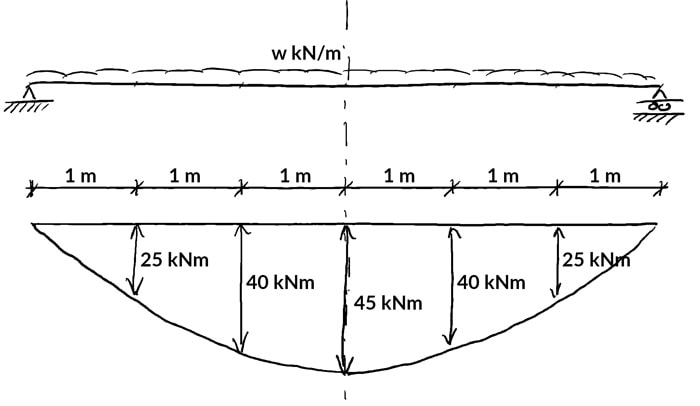
4.1 Finding the location of the maximum bending moment

In the example above, the structure and loading is symmetrical and then it'due south pretty easy to recognise the location of the maximum moment and so afterwards to evaluate it.

However this may non always be the case. So it'south helpful to take a technique to identify the location of the maximum moment without needing to plot the full bending moment diagram.

In this example, the bending moment for the whole structure is described by a unmarried equation…equation (12). Y'all might call up from basic calculus that to identify the location of the maximum betoken in a function we simply differentiate the function to get the equation for the slope. And then it's only a matter of setting this role equal to null and solving for 10.

In other words, at the location of the maximum bending moment, the slope of the angle moment diagram is zero. So we just need to solve for this location. In one case we take the location we tin can evaluate the angle moment using equation (12).

Then, to demonstrate let's get-go evaluate the differential of equation (12),

(13) $\begin{equation*} \frac{\mathrm{d}}{\mathrm{d}x} M(x) = \frac{wL}{2} - wx \end{equation*}$

Remember, equation (13) represents the gradient of the bending moment diagram. So we now let it equal to zip and solve for $x$ .

(14) $\begin{equation*} \frac{wL}{2} - wx = 0 \end{equation*}$

(fifteen) $\begin{equation*} \therefore x=\frac{L}{2} \end{equation*}$

Surprise surprise, the angle moment is a maximum at the mid-span, $x=L/2$ . At present we can evaluate equation (12) at $x=L/2 = 3$ m.

(16) $\begin{equation*} M(x=L/2) = \frac{wL^2}{4} - \frac{WL^2}{8} \end{equation*}$

(17) $\begin{equation*} \therefore M_{\text{max}} = \frac{wL^2}{8} = \frac{10\times 6^2}{8} = 45 \:\text{kNm} \end{equation*}$

There we have information technology; the location and magnitude of the maximum angle moment in this just supported beam, all with some basic calculus.

v.0 Drawing Shear Force and Bending Moment Diagrams – An Case

Now that we have a grasp of the fundamentals, let's run across how it all ties together with a bigger more complex worked case. This instance is an extract from this course. Just a quick heads up, if you're new to shear force and bending moment diagrams, this question might be a bit of a challenge. If you get a bit lost with this example, it might be worth your time taking a expect at this DegreeTutors course. It's aimed at bringing y'all from scratch all the way up to being comfortable analysing complex shear and moment diagrams.

Ok, let'south become on with it. Nosotros want to determine the shear force and bending moment diagrams for the following just supported beam.

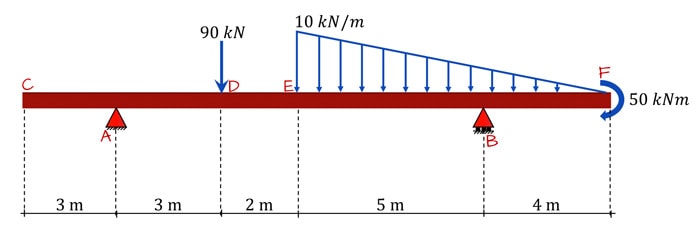
Shear-and-moment-diagrams-example-question| DegreeTutors.com

You tin can go on reading through the solution beneath…or if yous prefer video, you tin spotter me walk through the solution here.

5.1 Video Tutorial

five.two Calculating the support reactions

The start step in analysing whatsoever statically determinate structure is working out the support reactions. We can kick-off by taking the sum of the moments nigh point A, to decide the unknown vertical reaction at B, $V_B$ ,

(18) $\begin{equation*} \sum M_{\text{A}}=0\:\:\text{(assume clockwise positive)} \end{equation*}$

(19) $\begin{equation*} (90\text{kN}\times 3\text{m}) + 50\text{kNm} +(10\text{kN/m}\times 9\text{m}\times 8\text{m}\times 0.5) - 10\text{m}\times V_B = 0 \end{equation*}$

(20) $\begin{equation*} \therefore V_B = 68\text{kN} \end{equation*}$

Now with only i unknown force, nosotros can consider the sum of the forces in the vertical direction to summate the unknown reaction at A, $V_A$ ,

(21) $\begin{equation*} V_A + 68\text{kN} - 90\text{kN} - 10\text{kN/m}\times 9\text{m}\times 0.5 = 0 \end{equation*}$

(22) $\begin{equation*} \therefore V_A = 67\text{kN} \end{equation*}$

5.three Cartoon the shear forcefulness diagram

Our approach to drawing the shear strength diagram is actually very straightforward. We're going to 'trace the impact of the loads' across the beam from left to right.

The beginning load on the structure is $V_A = 67\text{kN}$ acting upwards, this raises the shear force diagram from zero to $+67\text{kN}$ at point A. The shear force and then remains constant every bit we move from left to correct until we hit the external load of $90\text{kN}$ acting down at D. This will crusade the shear force diagram to 'driblet' down by $90\text{kN}$ at D to a value of $+67 - 90 = -23\text{kN}$ .

This procedure of following or tracing the loads beyond the structure continues across the full beam until you've completely traced out the shear force diagram.

When nosotros achieve the linearly varying load at E, we brand apply of the human relationship between load intensity, $q$ and shear force $V$ that tells us that the slope of the shear force diagram is equal to the negative of the load intensity at a betoken,

(23) $\begin{equation*} \frac{\mathrm{d}V}{\mathrm{d}x} = -q \end{equation*}$

This is telling us that the linearly varying distributed load betwixt East and F volition produce a curved shear forcefulness diagram described by a polynomial equation. In other words, the shear force diagram starts curving at E with a linearly reducing gradient every bit we motility towards F, ultimately finishing at F with a gradient of null (horizontal). When the total loading for the beam is traced out, nosotros end upwardly with the post-obit,

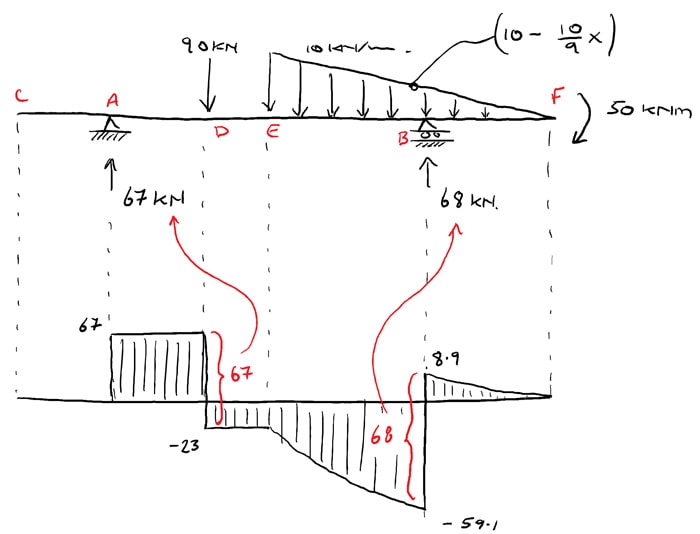
Shear-and-moment-diagrams-example-SFD| DegreeTutors.com

It'southward worth pausing for a moment to explicate how the shear force to the left of B, $V_{B,L} = -59.1\text{kN}$ was calculated. This is obtained by subtracting the total vertical load between E and B from the shear forcefulness of $-23 \text{kN}$ at Due east.

(24) $\begin{equation*} V_{B,L} = -23\text{kN}-(4.44\text{kN/m}\times 5\text{m}) - (10-4.44)\text{kN/m}\times 5\text{m}\times 0.5 \end{equation*}$

(25) $\begin{equation*} V_{B,L} = -59.1\text{kN} \end{equation*}$

5.iv Drawing the bending moment diagram

Once we've completed the shear forcefulness diagram, the bending moment diagram becomes much easier to determine. This is because we can brand utilise of the following relationship between the shear forcefulness $V$ and the gradient of the bending moment diagram,

(26) $\begin{equation*} \frac{\mathrm{d}M}{\mathrm{d}x} = V \end{equation*}$

Similarly to equation (23), this expressions allows u.s. to infer a qualitative shape for the bending moment diagram, based on the shear force diagram we've already calculated.

Consider the shear force between A and D for example; information technology's constant, which ways the slope of the angle moment diagram is also constant (an inclined straight line). Betwixt D and E, the shear force is nonetheless constant just has inverse sign. This tells us the slope of the bending moment diagram has also inverse sign, i.e. the bending moment diagram has a local top at D.

The fact that the shear force is a polynomial (curve) between E and F too tells the states the bending moment'due south gradient is continuously changing, i.e. it's also a curve. But the fact that the shear strength changes sign at B, means the angle moment diagram has a superlative at that point.

Finally, the externally applied moment at F tells u.s.a. that the bending moment diagram at this location has a value of $50\text{kNm}$ . We tin can combine all this information together to sketch out a qualitative bending moment diagram, based purely on the information encoded in the shear forcefulness diagram.

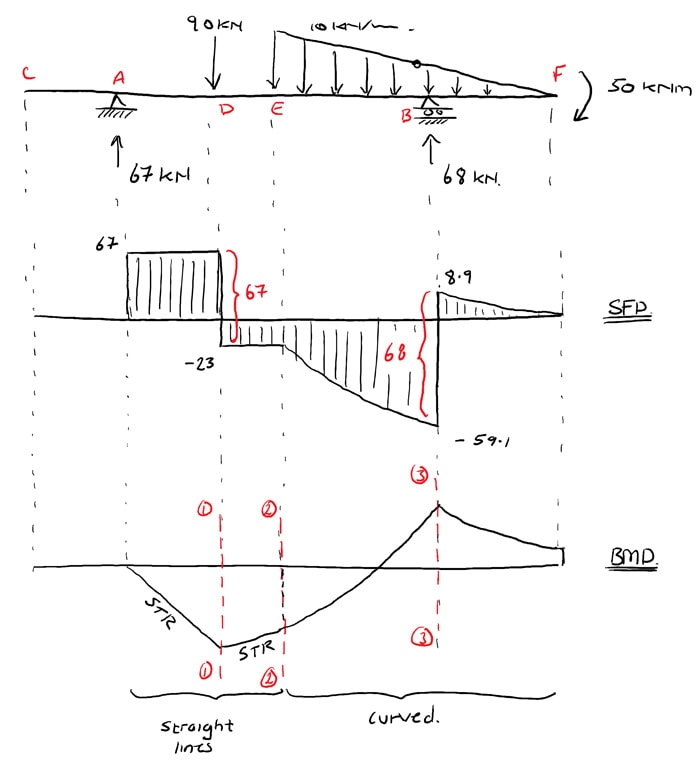
Shear-and-moment-diagrams-example-BMD-qualitative| DegreeTutors.com

Now nosotros only have to cut the structure at discrete locations (indicated with carmine dashed lines above) to establish the various key values required to quantitatively ascertain the bending moment diagram. In this case three cuts are sufficient:

at D to make up one's mind the local elevation – Cut ane-ane
at E to make up one's mind the value on the boundary between the directly and curved sections of the bending moment diagram – Cut two-2
at B to determine the local meridian – Cut 3-3

Cut ane-1

As nosotros've seen in a higher place, to make up one's mind the internal bending moment at D, $M_D$ , we cut the construction to reveal the internal bending moment at this point. Then by considering moment equilibrium of the sub-construction we can solve for the value of $M_D$ .

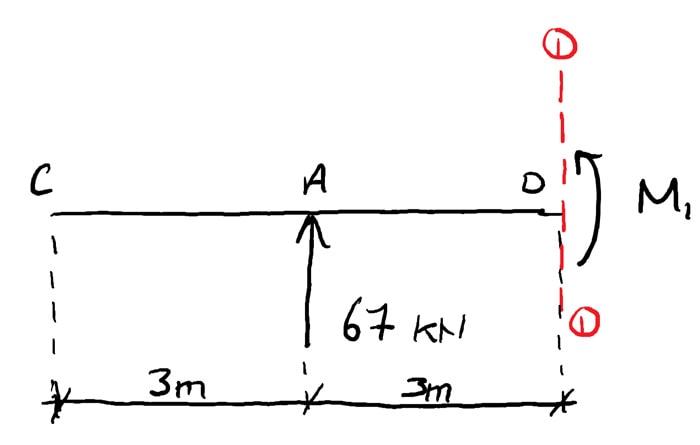
Shear-and-moment-diagrams-example-Cut-1| DegreeTutors.com

Taking the sum of the moments near the cut,

(27) $\begin{equation*} \sum M_{\text{cut 1}}=0\:\:\text{(assume clockwise positive)} \end{equation*}$

(28) $\begin{equation*} -M_1 + (67\text{kN}\times 3\text{m}) = 0 \end{equation*}$

(29) $\begin{equation*} M_1 = 201\text{kNm} \end{equation*}$

Cut 2-2

Repeating this process for cutting 2-2,

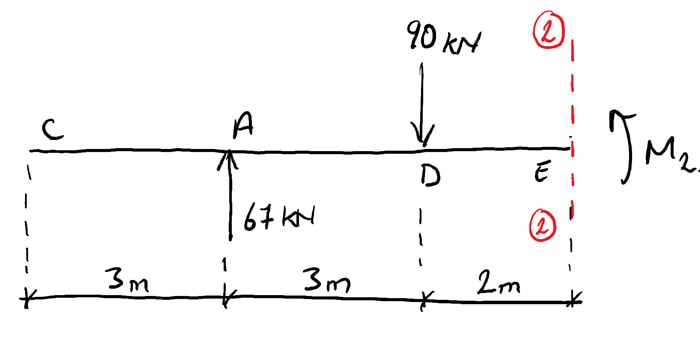
Shear-and-moment-diagrams-example-Cut-2| DegreeTutors.com

(thirty) $\begin{equation*} \sum M_{\text{cut 2}}=0\:\:\text{(assume clockwise positive)} \end{equation*}$

(31) $\begin{equation*} -M_2 + (67\text{kN}\times 5\text{m}) - (90\text{kN/m}\times 2\text{m}) = 0 \end{equation*}$

(32) $\begin{equation*} M_2 = 155\text{kNm} \end{equation*}$

Cutting three-three

And finally for cut 3-three, this time considering equilibrium of the sub-structure to the right-hand side of the cut

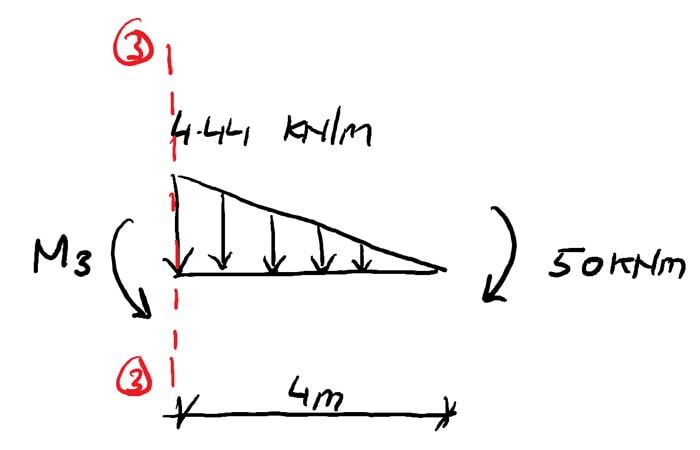
Shear-and-moment-diagrams-example-Cut-3| DegreeTutors.com

(33) $\begin{equation*} \sum M_{\text{cut 3}}=0\:\:\text{(assume clockwise positive)} \end{equation*}$

(34) $\begin{equation*} -M_3 + 50\text{kNm} + (4.44\text{kN/m}\times 4\text{m}\times 0.5 \times (4/3)\text{m}) = 0 \end{equation*}$

(35) $\begin{equation*} M_3 = 61.84\text{kNm} \end{equation*}$

Nosotros can now sketch the complete quantitative bending moment diagram for the structure. In fact at this signal we tin summarise the output of our complete structural analysis.

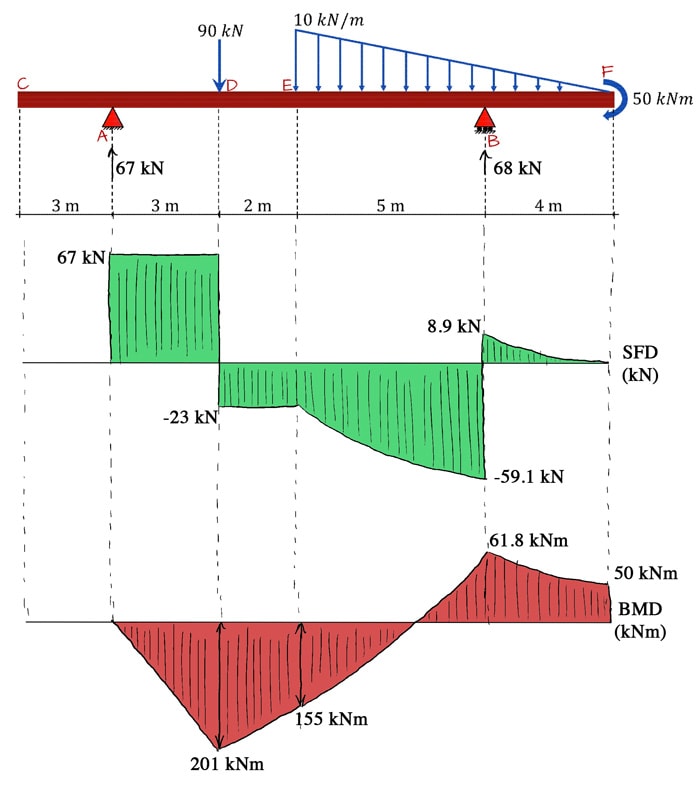
Shear-and-moment-diagrams-example-Summary-sketch| DegreeTutors.com

Later on working through this example, yous might exist interesting in this mail service, where we work through building a shear force and bending moment calculator using Python. Nosotros actually build our estimator effectually this case question – so definitely worth a read when you finish up with this mail.

half-dozen.0 Relating Loading, Shear Forcefulness and Bending Moment

In the previous instance, we fabricated use of 2 very helpful differential relationships that related loading with shear strength and shear force with angle moment. However we didn't properly innovate them. Now that we have a good idea of the general workflow for generating shear and moment diagrams, we can dig a chip deeper into these differential relationships. Understanding these, is the primal to being able to build shear force and bending moment diagrams quickly and reliably.

Fully agreement the relationships nosotros derive adjacent volition let you to more 'intuitively excerpt' qualitative shear and moment diagrams 'by heart', with cuts used to confirm numerical values at salient points. We're going to explore 3 cases:

Instance 1: Uniformly distributed loading
Example 2: Point force loading
Instance iii: Indicate moment loading

In each case, our objective is to decide the human relationship between the applied loading and the shear forcefulness and angle moment it induces.

6.1 Case 1: Uniformly distributed loading

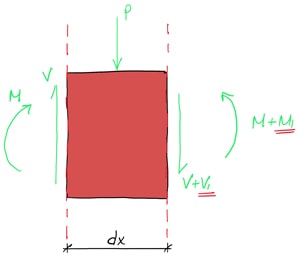
Consider a short segment of length $\mathrm{d}x$ cut from a beam and subject to a uniformly distributed load with intensity $w$ kN/m. As nosotros saw higher up, these cuts accept revealed the internal moment and shear on either side of the segment. Notation the infinitesimal increase in moment ( $\mathrm{d}M$ ) and shear ( $\mathrm{d}V$ ) on the right side of the cut.

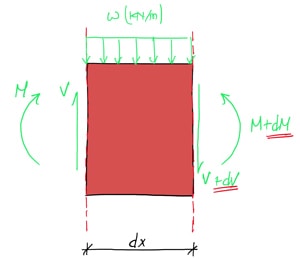
Beam segment with UDL | DegreeTutors.com

Shear Force

Nosotros can start by because vertical strength equilibrium for the segment. Since it must be in a country of static equilibrium, the sum of the vertical forces must equal zero.

$\begin{equation*}\sum F_y = 0\:\:(\uparrow+ve)\end{equation*}$

$\begin{equation*}V-(v+\mathrm{d}V)-w\mathrm{d}x=0\end{equation*}$

(36) $\begin{equation*}\therefore \boxed{ \frac{\mathrm{d}V}{\mathrm{d}x} = -w}\end{equation*}$

In other words, the slope of the shear force diagram $(\mathrm{d}V/\mathrm{d}x)$ at a point is equal to the negative of the load intensity at that bespeak. Nosotros tin demonstrate this with a unproblematic instance. Consider the axle below discipline to a distributed load with linearly increasing intensity. By making a cut at a distance $x$ from the left support with reveal the internal shear strength $V(x)$ .

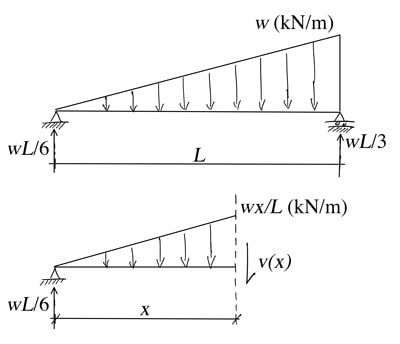
If the load intensity increases linearly from zero to $w$ , then at the cut the load intensity is $wx/L$ . We can at present evaluate vertical force equilibrium for the sub-structure,

$\begin{equation*}\sum F_y = 0\:\:(\uparrow+ve)\end{equation*}$

$\begin{equation*}V(x) = \frac{wl}{6} - \frac{wx^2}{2L}\end{equation*}$

We can now differentiate the expression for $V(x)$ yielding,

$\begin{equation*}\frac{\mathrm{d}V}{\mathrm{d}x} = -\frac{wx}{L}\end{equation*}$

So nosotros can see that the differential of the shear force is equal to the negative of the load intensity. Information technology'southward also worth noting the shape of the SFD, pictured below. At the left manus support when the load intensity is nil, the SFD has a value of $wL/6$ (the value of the left reaction) but information technology is horizontal, i.e. has a slope of nada. As the load intensity increases equally we move from left to right, the SFD gets steeper. i.e. the slope increases.

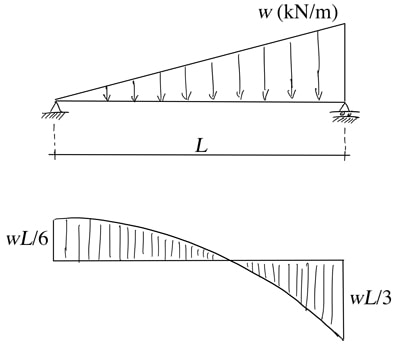
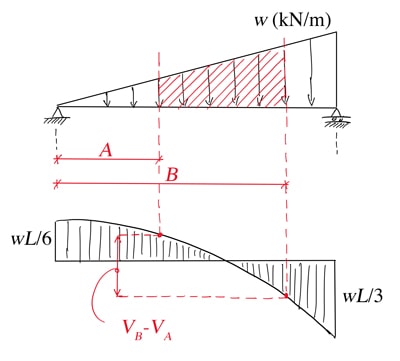
Another implication of this differential relationship between shear strength and load intensity tin can be seen if we integrate both sides of the equation,

$\begin{equation*}\frac{\mathrm{d}V}{\mathrm{d}x} = -w\end{equation*}$

$\begin{equation*}\int_A^B \mathrm{d}V = -\int_A^B w\: \mathrm{d}x\end{equation*}$

(37) $\begin{align*}V_B - V_A &= -\int_A^B w\: \mathrm{d}x\\&= - \:\text{area under loading diagram between A and B}\end{align*}$

We can come across this represented graphically in the epitome beneath.

Bending Moment

Having established the key relationship for shear, at present nosotros can turn our attention to bending moments. Referring back to our beam segment of length $\mathrm{d}x$ and considering moment equilibrium of the segment by taking moments well-nigh the left paw side of the segment,

$\begin{equation*}\sum M_{\text{LHS}} = 0 \:\:(\curvearrowright +ve)\end{equation*}$

$\begin{equation*}M-(M+\mathrm{d}M)+(V+\mathrm{d}V)(\mathrm{d}x)+w. \mathrm{d}x. \frac{\mathrm{d}x}{2} = 0\end{equation*}$

(38) $\begin{equation*}\therefore \boxed{ \frac{\mathrm{d}M}{\mathrm{d}x} = V}\end{equation*}$

So, the gradient of the BMD at a point equals the shear force at that point. Combined with the previous differential equation we derived, this is a very helpful equation. Whenever nosotros have a beam bailiwick to a distributed load, we can utilise these equations to infer the shape of the SFD and BMD. Consider the SFD and BMD for our beam beneath.

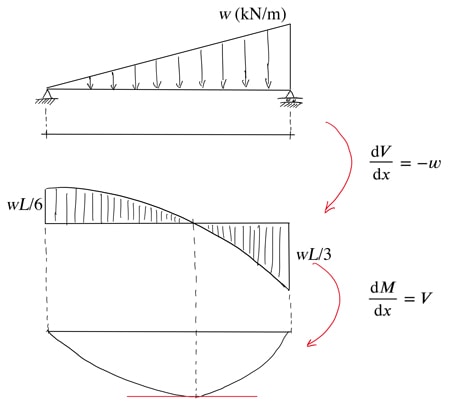
Nosotros note that when the shear forcefulness is zero, the gradient of the BMD is also zero indicating a local maximum in the BMD. We too note the change in sign of the gradient of the BMD as the shear force goes from positive to negative. Retrieve that the shape of the SFD was itself deduced from the shape of the loading diagram. Past making apply of these relationships betwixt loading, SFD and BMD, nosotros can build up a qualitative picture of structural behaviour.

half dozen.2 Case 2: Betoken force loading

Now we echo the same process as above but this time our axle segment is discipline to a bespeak load $P$ located at $\mathrm{d}x/2$ . Annotation that on the right hand side of the element, the internal shear force and angle moment have increased past a finite amount rather than an infinitesimal amount every bit was the instance previously.

Beam segment with point loading | DegreeTutors.com

Shear Force

Evaluating the sum of the vertical forces yields,

$\begin{equation*}\sum F_y = 0\:\:(\uparrow+ve)\end{equation*}$

$\begin{equation*}-P +V - (V+V_1)=0\end{equation*}$

(39) $\begin{equation*}\therefore \boxed{ V_1 = -P_1 }\end{equation*}$

From this we see that a point load induces a stride change in the SFD. Nosotros've already seen this when we followed the loads across the structure to build the shear strength diagram above. This equation is simply the mathematical representation of this. Consider for case the simple example beneath of a beam field of study to two betoken loads.

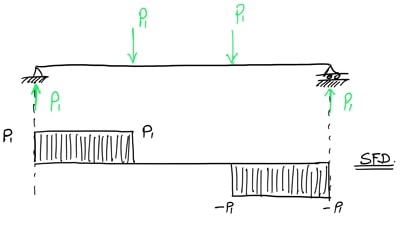
Beam with two point loads | DegreeTutors.com

Nosotros can readily run across the pace changes in the shear force diagram existence equal to the magnitude of the betoken loads at that location.

Bending Moment

If we at present consider moment equilibrium of our segment,

$\begin{equation*}\sum M_{\text{LHS}} = 0 \:\:(\curvearrowright +ve)\end{equation*}$

$\begin{equation*}M-(M+M_1) + P\frac{\mathrm{d}x}{2} + (V+V_1)\mathrm{d}x\end{equation*}$

$\begin{equation*}M_1 = \underbrace{P\frac{\mathrm{d}x}{2} + (V+V_1)\mathrm{d}x}_{\text{infinitesimally small}}\end{equation*}$

$\begin{equation*}\therefore \boxed{M_1 \approx 0}\end{equation*}$

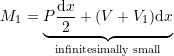
The presence of infinitesimally pocket-sized segment lengths on the right hand side of the equal sign ways that $M_1$ is infinitesimally small. From this nosotros conclude that the presence of a point load does not change the value of the bending moment diagram at a point.

Still, noting that the shear forcefulness changes from $V$ to $V-P$ , we can say, according to the expression,

(40) $\begin{equation*}\frac{\mathrm{d}M}{\mathrm{d}x} = V\end{equation*}$

that the slope of the angle moment diagram changes by an amount $P$ . Over again, we can meet how this maps onto our simple instance beneath. Note that at the point of application of $P_1$ , the slope of the bending moment diagram changes. Too, where the shear strength is cipher, the bending moment diagram is horizontal.

So we have added two more equations into our toolbox for establishing qualitative structural behaviour.

Beam with two point loads and diagrams | DegreeTutors.com

6.3 Case iii: Indicate moment loading

Finally nosotros can echo the analysis for the case of moment applied at a point.

Beam segment with point moment | DegreeTutors.com

Shear Force

Take the sum of the forces in the vertical direction,

$\begin{equation*}\sum F_y = 0\:\:(\uparrow+ve)\end{equation*}$

$\begin{equation*}V-(V+V_1)\end{equation*}$

$\begin{equation*}\therefore \boxed{V_1 = 0}\end{equation*}$

And so, the shear strength diagram does not change with the application of a moment.

Bending Moment

Taking the sum of the moments nearly the left mitt side of the cut,

$\begin{equation*}\sum M_{\text{LHS}} = 0 \:\:(\curvearrowright +ve)\end{equation*}$

$\begin{equation*}M+M_o-(M+M_1)+\underbrace{(V+V_1)\mathrm{d}x}_{\text{infinitesimally small}\rightarrow 0} = 0\end{equation*}$

$\begin{equation*}\therefore \boxed{M_0 = M_1}\end{equation*}$

This ways that at the indicate of application of a angle moment, there is a step change in the bending moment diagram, equal to the magnitude of the moment applied.

The 6 boxed equations in this department above can exist used to infer a huge amount of data almost the behaviour of a structure under load. Allow's put this into exercise with another worked instance.

vii.0 Some other Example

Determine the shear strength diagram and angle moment diagram for the following simply supported beam. Make sure to attempt this yourself before watching the solution videos.

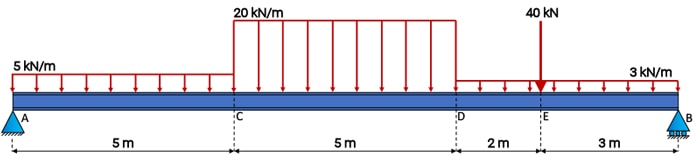
Shear and moment example | DegreeTutors.com

7.ane Setup and shear strength diagram

seven.2 Building the angle moment diagram

7.iii Confirming maximum moment with calculus

So there you take information technology. We've linked together the internal normal and shear stresses with the bending moment and shear force diagrams. And we've derived a toolbox full of helpful differential equations to assistance us quickly and intuitively build shear force and bending moment diagrams. In that location is quite a lot more nosotros could say about shear and moment diagrams. But that's probably enough for one post.

The best mode for y'all to go better at evaluating shear strength and bending moment diagrams is through practice. At that place actually are no shortcuts I'thou afraid. The good news is, the more you practice, the quicker you get and the stronger your intuition for structural behaviour becomes. That's all for now, I hope you lot got some value from reading this mail service and I'll run into you lot in the next one.

Build your own shear force and bending moment solver

Understanding how to build shear force and bending moment diagrams the way we've demonstrated in a higher place is an essential skill. Even so, the process is fourth dimension consuming, particularly when you enter the iterative process of analysis and design. And that's earlier we even start talking about how to handle indeterminate structures! For these reasons, we generally make utilise of structural analysis software to speed the process up. But this software is typically expensive and for the vast majority of cases, has way more functionality than we demand. And so – why non just build y'all own, for (almost) complimentary! In my course beneath, nosotros use the Direct Stiffness Method to build our own 2d beam and frame analysis programme using Python. You don't need to be a developer to take this course. When yous're finished it…yous'll have your own DIY structural analysis plan.