how to draw the derivative of a graph

GRAPHING OF FUNCTIONS USING Outset AND Second DERIVATIVES

The post-obit problems illustrate detailed graphing of functions of one variable using the first and second derivatives. Bug range in difficulty from average to challenging. If you are going to endeavor these problems before looking at the solutions, you tin avoid common mistakes by carefully labeling critical points, intercepts, and inflection points. In addition, it is important to label the distinct sign charts for the first and 2nd derivatives in club to avoid unnecessary defoliation of the post-obit well-known facts and definitions.

Here are teaching for establishing sign charts (number line) for the first and second derivatives. To establish a sign chart (number lines) for f' , first set f' equal to zero and then solve for ten . Mark these x-values underneath the sign nautical chart, and write a goose egg higher up each of these 10-values on the sign chart. In addition, mark ten-values where the derivative does not be (is not divers). For example, mark those ten-values where division by zippo occurs in f' . To a higher place these x-values and the sign chart draw a dotted vertical line to indicate that the value of f' does not exist at this point. These designated x-values found intervals along the sign chart. Next, choice points between these designated x-values and substitute them into the equation for f' to determine the sign ( + or - ) for each of these intervals. Beneath each designated 10-value, write the corresponding y-value which is constitute by using the original equation y = f(x) . These ordered pairs (10, y) will be a starting indicate for the graph of f . This completes the sign chart for f' . Establish a sign chart (number line) for f'' in the exact same manner. To avert overlooking zeroes in the denominators of f' and f'' , it is helpful to rewrite all negative exponents equally positive exponents and so advisedly manipulate and simplify the resulting fractions.

FACTS and DEFINITIONS

$\uparrow$

2. If the first derivative f' is negative (-) , and so the function f is decreasing ( $\downarrow$ ) .

3. If the second derivative f'' is positive (+) , then the function f is concave upward ( $\cup$ ) .

4. If the second derivative f'' is negative (-) , and then the function f is concave down ( $\cap$ ) .

v. The signal x=a determines a relative maximum for function f if f is continuous at ten=a , and the first derivative f' is positive (+) for x<a and negative (-) for x>a . The point 10=a determines an absolute maximum for office f if it corresponds to the largest y-value in the range of f .

6. The signal ten=a determines a relative minimum for role f if f is continuous at x=a , and the first derivative f' is negative (-) for x<a and positive (+) for ten>a . The point 10=a determines an absolute minimum for part f if it corresponds to the smallest y-value in the range of f .

7. The point ten=a determines an inflection point for function f if f is continuous at ten=a , and the second derivative f'' is negative (-) for x<a and positive (+) for x>a , or if f'' is positive (+) for x<a and negative (-) for x>a .

eight. THE Second DERIVATIVE TEST FOR EXTREMA (This tin can be used in place of statements five. and 6.) : Assume that y=f(x) is a twice-differentiable function with f'(c)=0 .

a.) If f''(c)<0 so f has a relative maximum value at x=c .

b.) If f''(c)>0 then f has a relative minimum value at ten=c .

These are the directions for problems i through 10. For each part land the domain. Decide all relative and absolute maximum and minimum values and inflection points. State conspicuously the intervals on which the function is increasing ( $\uparrow$ ) , decreasing ( $\downarrow$ ) , concave up ( $\cup$ ) , and concave downwards ( $\cap$ ) . Make up one's mind x- and y-intercepts and vertical and horizontal asymptotes when appropriate. Neatly sketch the graph.

Problem ane : Do detailed graphing for f(x) = x ⁱⁱⁱ - 3x ² .

Click HERE to see a detailed solution to problem 1.
PROBLEM ii : Practice detailed graphing for f(x) = x ^four - fourx ³ .

Click HERE to see a detailed solution to trouble 2.
PROBLEM three : Do detailed graphing for f(x) = x ^three (x-2)² .

Click HERE to see a detailed solution to problem 3.
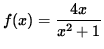Trouble 4 : Do detailed graphing for $f(x) = \displaystyle{ 4x \over x^2 + 1 }$ .

Click Here to see a detailed solution to problem 4.
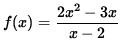PROBLEM v : Do detailed graphing for $f(x) = \displaystyle{ 2x^2-3x \over x-2 }$ .

Click Here to see a detailed solution to problem 5.
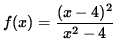Trouble vi : Practise detailed graphing for $f(x) = \displaystyle{ (x-4)^2 \over x^2 - 4 }$ .

Click Here to see a detailed solution to problem 6.
PROBLEM 7 : Do detailed graphing for f(10) = x - 3x ^1/3 .

Click HERE to come across a detailed solution to trouble 7.
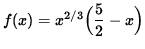PROBLEM 8 : Practice detailed graphing for $f(x) = x^{2/3} \Big( \displaystyle{ 5 \over 2 } - x \Big)$ .

Click HERE to see a detailed solution to trouble 8.
Problem 9 : Practise detailed graphing for 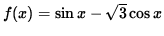$f(x) = \sin x - \sqrt{ 3 } \cos x$ for ten in $[0, 2\pi ]$ .

Click Here to see a detailed solution to trouble 9.
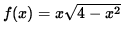Trouble 10 : Do detailed graphing for $f(x) = x \sqrt{ 4 - x^2 }$ .

Click Hither to encounter a detailed solution to trouble 10.
PROBLEM xi : Consider the cubic polynomial y = A 10 ³ + 6x ² - Bx , where A and B are unknown constants. If possible, determine the values of A and B and so that the graph of y has a maximum value at x= -ane and an inflection point at 10=ane .
Click Hither to see a detailed solution to problem 11.